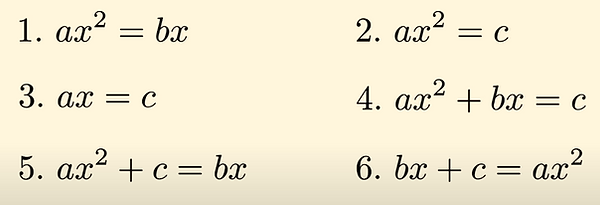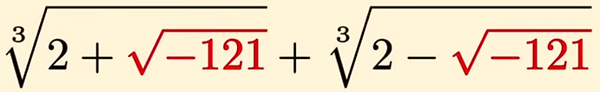How Imaginary Numbers Were Invented
Ela Nur Halil
Luca Pacioli, Leonardo da Vinci’s math teacher published Summa de Arithmetica in 1494. It consisted of all math known in Renaissance Italy. One chapter was devoted to the cubic equation. Pacioli came to the conclusion that solving it was impossible.
Many ancient civilizations in the past such as the Babylonians, Greeks, Indians, and Egyptians had encountered it, but all of them had failed at their attempt to solve the cubic. The quadratic equation, however, had been solved many separate times before using the method of completing a square.
16 is 4 squared so we can infer that x+3=4, x=1. However, 1 is not the only root of this equation. -7 is also a solution for this equation. For years, mathematicians were oblivious to the negative roots of their equations because they relied on geometry so much. After all, a square with side lengths -7 doesn’t make sense. In the past, there was no unified quadratic equation. There were 6 quadratics arranged so that the coefficients were always positive:
The same approach was taken by Persian mathematician Omar Hayyam in the 11th century. He identified 19 forms of the cubic, again keeping all the coefficients positive. He managed to solve some of the equations by considering the intersection of some shapes but fell short of his ultimate goal of finding a general solution to the cubic.
Scipione del Ferro was a mathematics professor at the University of Bologna. Around 1510, he found a way to solve the depressed cubic, a cubic equation without the second-degree term, yet he didn’t share his method with anybody because competition between mathematicians was very fierce at the time. Any mathematician was able to show up and challenge you for your position. In order to determine who was better, each would give the other a set of problems to solve. The one who solved the most problems would be victorious and the other would suffer public humiliation.
On his deathbed in 1526, del Ferro revealed his method to his student Antonia Fior. After del Ferro’s death, Fior claimed to have found a way to solve the depressed cubic and boasted about his mathematical capability. In 1535, Fior challenged Niccolò Fontana Tartaglia. Tartaglia was an Italian mathematician who grew up in poverty and was therefore mostly self-taught. He had worked very hard to become a respected mathematician and now all of this was at stake. Each mathematician gave the other 30 problems. Fior gave Tartaglia only depressed cubics. Tartaglia was able to solve all of Fior’s depressed cubics while Fior wasn’t able to solve any of Tartaglia's problems.
Tartaglia wasn’t convinced of Fior’s ability to create such a rule to solve the depressed cubic in the first place and now, his suspicions were confirmed to be somewhat true. Word got out that a great mathematician had revealed this rule to Fior. With the knowledge that solving the depressed cubic was possible, Tartaglia set out to find a general solution to the depressed cubic.
Tartaglia found a general solution to the depressed cubic by completing the square used in the quadratic to a cube. Here is an example of how he solved it:
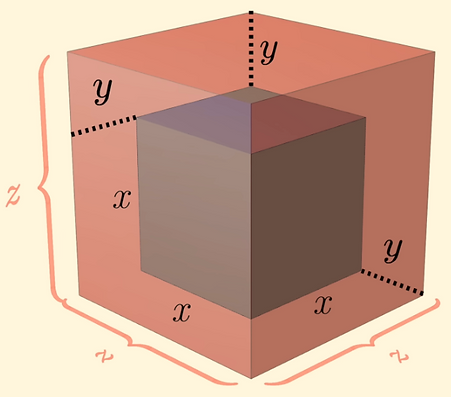
Tartaglia thought of the third-degree term as a cube with side lengths x. If you increase the side lengths by y, you get a cube with side lengths x+y. Let’s say x+y equals to z.
If you dissect the cube into 8 pieces, you get one piece with a volume of x^3, one with y^3, 3 with yx^2, and finally 3 with xy^2.
Tartaglia rearranged these pieces so that the pieces whose volumes were yx^2 and xy^2 formed a block.
He wanted this block to represent 9x. And if this block represents 9x, its base must be 9. Therefore 3yz = 9, yz = 3, z = 3/y.
In order for this equation to represent the whole cube, we have to add y3 to both sides. This way, both sides of the equation are equal to z^3.
We know that z = 3/y so we can derive this from this equation:
This may look more complicated than where we started, but if you think of y^3 as a new variable, it’s actually a quadratic equation.
If you solve this quadratic equation y^3 is equal to 1, therefore y=1. Z is equal to 3/y so z=3. Z-y=x therefore x=2.
After solving the depressed cubic, Tartaglia became the second human on Earth to do so. Instead of going through the geometry for each cubic he encounters, he wrote a poem to describe the set of instructions he used to solve the depressed cubic.
This made him a celebrity, but Tartaglia refused to reveal his method to anyone, wanting to maintain his position. Everyone was very curious about his method, especially Gerolama Cardano who was a polymath based in Milan. Cardano wrote a series of letters to Tartaglia, almost begging him to reveal his method. After some time Cardano lured Tartaglia to Milan with the promise of an introduction to his method. In 1539 Tartaglia revealed his method to Cardano, but he made him promise not to tell anyone and only to write it in cipher.
Cardano played around with Tartaglia’s method for a while, but his ultimate goal was to solve the cubic equation with the x^2 term, which he did. He substituted the x variable for x-b/3a . This canceled out all the x^2 terms, leaving a depressed cubic which could be solved with Tartaglia’s method.
Cardano was ecstatic to have solved the problem that had stumped the best mathematicians for decades, but he couldn’t publish it because of his oath to Tartaglia. He had no problem publishing it because he made his living as a physician, not as a mathematician.
In 1542, Cardano traveled to Bologna and met the son-in-law of Scipione del Ferro. During his visit, he found a solution to the cubic predating Tartaglia’s by decades in del Ferro’s old notebook, which gave Cardano a way to publish the solution without violating his promise to Tartaglia.
In 1545, Cardano published Ars Magna. The book contains a unique geometric proof of 13 arrangements of the cubic. Tartaglia was, of course, furious about this and wrote Cardano a series of letters expressing his anger.
While writing Ars Magna, Cardano encountered some cubic equations which couldn’t be solved in the usual way. Here is an example:
The solution to this problem involves the square roots of negative numbers.
However, if you do a little guessing and checking you can find out that 4 is one of the roots of x. Cardano didn’t understand why he couldn't find a reasonable solution to this problem. He dismisses this case in Ars Magna by calling the square roots of negatives “as subtle as [they are] useless.”
Cardano asks Tartaglia about this case. Tartaglia tells him that he isn’t clever enough to utilize his method correctly. However in reality Tartaglia couldn’t understand this case either.
Cardano looks back on the geometric proof of a similar problem. He has no problem completing the cube but in the step of solving the quadratic equation, he encounters a geometrical paradox.
Cardano finds a part of a square which is equal to 30. The side lengths of the square are equal to 5. Therefore the remaining area must be equal to -5, but there is no such thing as negative area.
Around ten years later Rafael Bombelli, an Italian engineer picks up where Cardano left off. He defines square roots of negative numbers as their own new type of number and tries to work with them. Bombelli assumes that the terms in Cardano’s solution can be represented as a combination of an ordinary number and this new type of number which involves the square root of -1.
When he takes the final step and adds the terms together, he finds out that the square roots of -1 cancels out and the sum is equal to 4. Cardano’s method does work but you have to ignore the geometric proof which generated it in the first place.
In the 1600s, François Viète introduced modern symbolic notation of algebra, ending the tradition of math problems as drawings and wordy descriptions. René Descarted popularized the square roots of negatives by using them quite a lot. He called them imaginary numbers and this name stuck. Leonhard Euler later introduced i to represent the square root of -1. Combined with regular numbers they form complex numbers.
The cubic led to the invention of a new type of number and the separation of algebra from geometry. This way, geometry was no longer the source of truth. By letting go of geometry which describes what we can see and touch, we get a much better grasp of reality.
The cubic was just the beginning of the utilization of imaginary numbers. In 1945, Erwin Schrödinger released a wave equation called the Schrödinger equation which described the behavior of quantum particles. i is featured prominently within this equation.
Physicists were uncomfortable with i showing up in such a fundamental equation, but later on physicist Freeman Dyson stated that the use of i was what separated the equation from a heat conduction equation. He said that this equation describes everything we know about atoms correctly, and most importantly that nature works with complex numbers and not with real numbers.
To summarize everything discussed in this article, imaginary numbers were invented in order to solve the cubic equation. However, they are much more important than we think they are. Imaginary numbers come up in the Schrödinger equation, which is fundamental for understanding how the universe works.
References
Veritasium. 1 Nov. 2021, “How Imaginary Numbers Were Invented” [video] Youtube https://www.youtube.com/watch?v=cUzklzVXJwo
Branson, William, “Solving the Cubic with Cardano”, 2014, accessed Nov. 17 2023 https://maa.org/press/periodicals/convergence/solving-the-cubic-with-cardano
Merino, Orlando, “A Short History of Complex Numbers”, 2006, accessed Nov. 18 2023 https://math.mit.edu/~dunkel/Teach/18.04_2019S/historic/Merino_2006.pdf
Figure References
[3] [4] [5] [6] [7] [8] [9] [11 ] Via Veritasium. 1 Nov. 2021, “How Imaginary Numbers Were Invented” [video] YouTube https://www.youtube.com/watch?v=cUzklzVXJwo
[1] [2] [12] designed by the author Ela Nur Halil
[10] https://www.facebook.com/Thinkerium/photos/a.495827023809984/4617363674989611
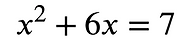


In the equation shown above, x^2 represents a square with side lengths x. 6x represents a rectangle with side lengths 6 and x. In order to solve this equation, mathematicians would divide the rectangle into 2 identical rectangles with side lengths 3 and x, forming a square with side lengths x+3. In order to complete the square, you had to add 9 to x+6x because (x+3)^2 is equal to x^2 + 6x + 9. In order to make both sides of the equation equal, you had to add 9 to 7 making the right side equal to 16. This way, the equation would look something like this: